Rubi - A Rule-based Integrator for Mathematical Expressions

If you never heard of Rubi, then you might want to stop here and take a quick look over the Rule-based Integration website before reading the rest of the post.

The Beginning

About two months ago, I came across a post on the Wolfram Community about a project called Rubi. I had already heard about it, and I knew that it aims to solve integrals by applying mathematical rules to find the antiderivative of an expression step by step.

Usually, I can solve my integrals on paper or with the help of Mathematica, and if it’s indeed too hard to solve analytically, I draw the big numerical guns to get the job done. However, what I found intriguing was that with Rubi you could view all steps along the way and for each step, you can inspect the conditions that are required to make the transformation valid and useful. That is something you cannot get out of Mathematica easily (with Wolfram Alpha this works sometimes) and to know how an antiderivative is found is very enlightening if you genuinely want to understand things.

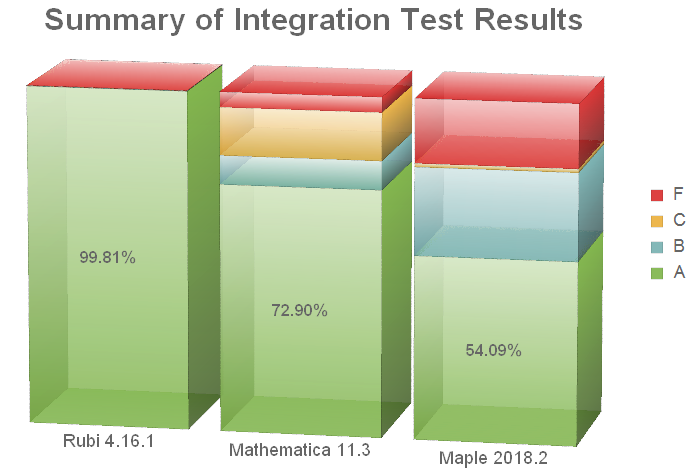
The other thing that caught my attention was that Rubi seemed to be backed by a vast number of integration tests to ensure the quality of the antiderivatives it produces. Rubi’s performance is validated by 70.000+ test cases, where each test case consists of an integration problem and its optimal solution. I was astounded to find out how many integrals Rubi can solve. Here is a plot from the Rubi website that ranks the test-cases in comparison to other computer algebra systems.

Meeting Albert Rich

I took a night off to look over the sources of Rubi and found that besides the many integration rules, the code to wrap this into a Mathematica package was of moderate size. On a closer look, I found things that I could definitely improve to make Rubi more accessible as a package. In addition, although Rubi was open-source, it was hosted on a private website which is not quite the state of the art in times of GitHub. Especially, when you try to get people to participate, report bugs, help with the documentation or let them make feature-suggestions. Then, it is better to have everything easily accessible and GitHub’s mix of tools containing an issue-tracker, project websites, and repository wikis provides a good package.

After my first assessment, I gave this some thought and wrote a detailed answer of what I had in mind for Rubi. Some days went by and one morning I had a email from Albert who started by expressing his fondness for the George Carlin quote on my website ‘People who see life as anything more than pure entertainment are missing the point.’ He also really liked my ideas and would dearly appreciate some help on the project.

We devised a plan that included to keep Albert out of setting up a new website, creating repositories, etc., so he could concentrate on the math. But I knew from the start I couldn’t keep him completely out of the game. For one, there were many things to discuss as I needed a pretty good overview of Rubi to understand Albert’s intentions. Secondly, I did not want to publish Rubi on my GitHub account because it is Albert’s work and I didn’t want to take credit for this.

Setting up a GitHub organization

After some discussion over email, I had a pretty large working plan on my schedule and I basically started right away leaving my other free-time projects in the drawer for a while. I began by creating the Rule-based Integration Organization on GitHub since this seemed to be the most reasonable way to

1. have several repositories under the same roof
2. have a dedicated organization website for Rubi
3. have Albert and other collaborators visible to others and give them access to the repositories

“Why do you need several repositories?”, you might ask. Because Rubi is not bound to the Wolfram Language and the integration rules can be viewed as PDF or implemented in any computer algebra system with sufficient support for transformations based on expressions. Therefore, I wanted to separate the plain rules from the Mathematica package. In addition to Mathematica, the large test-suite of 70.000+ integration problems is available for Axiom, Maple, and Maxima as well and I wanted a clear separation.

I decided to make the Rule-based Integration website as a GitHub page for the organization with one of GitHub’s supported Jekyll schemes. That had a huge advantage: It is built automatically, and Albert, who never worked with git (or Jekyll) could write content and make changes by merely editing the markdown files online (just like you can do it in the GitHub wiki as well).

My evil secret plan was to bring Albert slowly up to speed and make this “new technology” so easy for him that I could get some of the work off my back. Fortunately, Albert was a willing patient, and before I knew it, we were chatting on Gitter almost daily, and I could send him into the battle of (re)writing content in markdown while I could think about what to do with the Mathematica package.

The Mathematica package

Albert already had a working package that could be used from inside its directory, but I thought some details could relatively easily be improved. First of all, there is a PacletManager in Mathematica that lets you install, update and remove packages directly from an online resource. Although there is still no official documentation available, we found out most things about the PacletManager ourselves. Therefore, the goal was to have the Rubi releases directly on GitHub and make it possible for users to install them from there directly.

The second thing I took care of is the view of the integration steps and the integration statistics. The old implementation printed cells during the run which had some serious issues when you re-evaluated a computation. Also, I wanted to improve the style of the output and modernize it a bit. Therefore, you will find a beautiful dynamic panel that shows you information about each integration step in the current release:

The last important thing for me was the workflow of how the Rubi rules are extracted into the package. You should know that Rubi’s notebook source files contain not only the Mathematica code for each of the 6600+ rules, but the corresponding formula and application conditions expressed in standard 2-D mathematical notation. Also reference and derivation information for each rule is provided when known. Thus Rubi’s source files provide a comprehensive, human readable repository of concise and precise knowledge required to symbolically integrate large classes of mathematical expressions. Therefore Rubi’s website makes the source files available as pdf files as well as Mathematica notebook files. For the Mathematica package, however, we only need the plain source code from each rule.

Until recently, this was done manually by Albert who exported every notebook into a package file and joined similar ones. Since this is a waste of Albert’s time and a tedious procedure, I automated this step with Mathematica which is able to load notebooks and extract the code with

NotebookImport[file, "Code" -> "HeldExpression"]

So with some 20 lines of Mathematica code, it was possible to extract all rules from the notebooks and pack them into the dense package files that are loaded.

What’s left to be done?

Some things still need to be polished. The loading time of the package is awful because the files with the rules are large. Very large. This can be vastly improved by storing them in the binary .mx format but this needs some serious thinking. First of all, this format is not compatible between all versions and operating systems, so it’s best to create them on the user’s machine during the first loading of the package.

However, there is another difficulty. When you ask Rubi to show the integration steps, we inject code into each integration rule that collects information about the step. Currently, this is done during the loading of the package if you set the global variable $LoadShowSteps = True. The best case would be if neither of this was required: No long loading time and no global variables.

Finally, there is one significant entry on the wish-list which unfortunately requires a severe rework of how integration-step information are injected in Rubi. Wouldn’t it be nice to not only see the steps of integration but to be able to interactively open the exact position in the source notebook that contains so much more mathematical information about the rule? I truly believe this would be a great feature and I already have a rough plan for how this might be implemented. However, an idea is an idea and time to work on this lives currently on a different planet.

That brings me to my final paragraph, where I don’t want to miss the opportunity to say that if you are interested in Rubi, have a decent knowledge of meta-programming in Mathematica, and would like to jump on board, feel free to visit the Rubi Gitter chat. If you only want to use Rubi, please visit rulebasedintegration.org and read how it can be installed and used.